Lásd
még:
Henger
A hasáb olyan test, amelyet két egybevágó sokszöglap és annyi
paralelogramma határol, ahány oldala van a sokszögnek. A két egybevágó
sokszög a hasáb
alapja,
(alaplapja) illetve a
fedőlapja, a többi a hasáb
oldallapja.
Az alapokat határoló élek az
alapélek.
Az oldallapok az
oldalélekben
találkoznak. Az oldallapokat együtt a hasáb
palástjának
nevezzük.
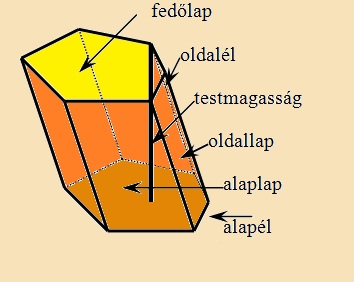
Testmagasság:
az alaplap és a fedőlap távolsága. |
Példa:
|
 |
|
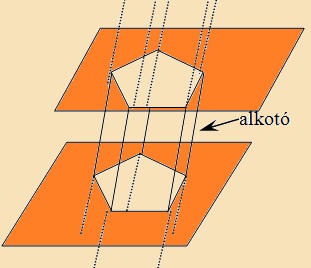
Hasábfelületet
kapunk, ha egy síkbeli sokszög pontján át párhuzamosokat húzunk egy
egyenessel. Ha ezt a hasábfelületet az adott síkidom síkjával párhuzamos
és egy vele párhuzamos másik síkkal elmetsszük, egy
hasábot kapunk. A két
egybevágó sokszögvonal pontjainak távolsága a hasáb
alkotói.
Így az oldalélek is alkotók. |
Példa: |
 |
|
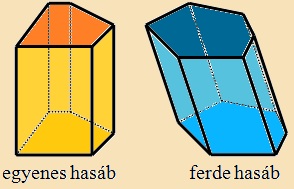
Ha a hasáb oldalélei merőlegesek az alapra,
egyenes hasábról
beszélünk, ilyenkor az oldallapok téglalapok. Ha a hasáb oldalélei
nem merőlegesek az alapra
ferde hasábról
beszélünk. Az egyenes hasáboknál az alkotó és a testmagasság egyenlő
hosszú. |
Példa: |
 |
A kocka és a téglatest is hasáb. A kocka szabályos hasáb, (szabályos
test).
Az n oldalú hasábnak (n+2)
számú lapja,
2n
számú csúcsa és
3n számú éle van. A lapok (l),
csúcsok (c) és élek (é)
között a következő összefüggés figyelhető meg: l + c
= é +2.
Az egyenes hasáb palástja olyan téglalap, melynek egyik oldala az alap
kerülete, a másik oldala a testmagasság. |
|
Az
egyenes hasáb felszínét
úgy kaphatjuk meg, hogy az alapterületének kétszereséhez hozzáadjuk
palást területét, (alap kerületének és a testmagasságának a szorzatát). |
Képlettel: |
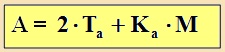 |
|
Az
egyenes hasáb térfogatát
úgy kaphatjuk meg, hogy az alap területét szorozzuk a hasáb
magasságával. |
Képlettel: |
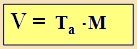 |
| |
|
|
|