|
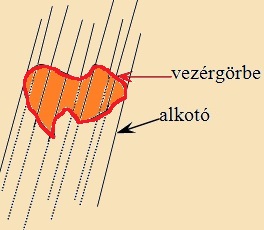
Ha egy egyenest valamely görbe mentén úgy mozgatunk, hogy a mozgás
közben eredeti helyzetével párhuzamos marad, akkor az egyenes
hengerfelületet
ír le. A görbét
vezérgörbének,
az egyenest és a vele párhuzamos egyeneseket
alkotónak
nevezzük. Ha ezt a hengerfelületet párhuzamos síkokkal elmetsszük, egy
hengert kapunk. A párhuzamos
síkok és a hengerfelület által közbezárt síkidomok a henger
alapja,
illetve a
fedőlapja, a többi része a
palást. |
Példa:
|
 |
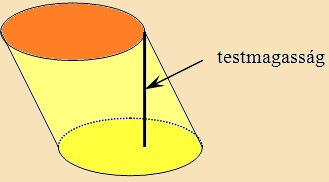
Testmagasság:
az alaplap és a fedőlap távolsága.
Ha a vezérgörbe kör, akkor
körhengerről beszélünk. |
Példa:
|
 |
|
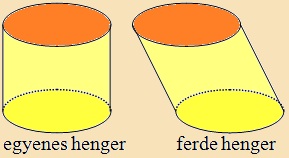
Ha a henger alkotói merőlegesek az alapra,
egyenes hengerről
beszélünk, ilyenkor a palást egy téglalap. Ha a henger alkotói
nem merőlegesek az alapra
ferde hengerről
beszélünk. Ha az egyenes henger vezérgörbéje kör, akkor
egyenes körhengerről
beszélünk. Az egyenes hengereknél az alkotó és a testmagasság egyenlő
hosszú. |
Példa: |
 |
|
Az egyenes körhenger
palástja olyan téglalap, melynek egyik oldala az alap kerülete, a másik
oldala a testmagasság. |
Példa: |
 |
A
hasáb olyan henger, melynek alaplapja és
fedőlapja egybevágó sokszög.
|
Az
egyenes körhenger felszínét úgy kaphatjuk meg, hogy az alap területének kétszereséhez hozzáadjuk az
alap kerületének és a testmagasságának a szorzatát.
Behelyettesítve a kör kerület és terület képletét:
A =
2
· Ta
+ Ka · M = 2r2Π + 2rΠ
· M = 2rΠ
(r + M) |
Képlettel: |
 |
Az
egyenes körhenger térfogatát
úgy kaphatjuk meg, hogy az alap területét szorozzuk a hasáb magasságával.
Behelyettesítve a kör kerület és terület képletét:
A =
2
· M = 2r2Π
· M
|
Képlettel: |
 |
| |
|
|
|