|
Kúpfelületet
ír le az olyan egyenes, amely egy adott görbe mentén mozog oly módon,
hogy közben az egyik pontja állandóan rögzített marad. A rögzített
pontot
csúcspontjának
(csúcs)
nevezzük, a görbét
vezérgörbének
az egyeneseket
alkotónak.
Ha ezt a kúpfelületet egy síkkal elmetsszük, egy
kúpot kapunk. A vezérgörbe
által bezárt síkrész a kúp
alapja,
a többi része a
palást. |
Példa:
|
 |
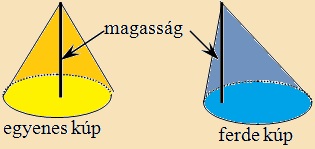
Testmagasság:
az alaplap és a csúcs távolsága.
Ha a vezérgörbe kör, akkor
körkúpról
beszélünk.
Ha a kúp magasságának talppontja az alap középpontjában van,
egyenes kúpról
beszélünk. Ha a kúp magasságának talppontja nem
az alap középpontjában van
ferde kúpról
beszélünk. Ha az egyenes kúp vezérgörbéje kör, akkor
egyenes körkúpról
van szó. |
Példa: |
 |
|
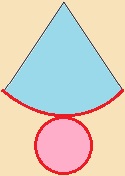
Az egyenes körkúp palástja egy olyan körcikk, melynél a körív hossza
megegyezik az alapkör kerületével. |
Példa: |
 |
|
A
gúla
olyan kúp, melynek alaplapja sokszög. |
|
A
kúp felszínét
úgy kaphatjuk meg, hogy az alap területéhez hozzáadjuk a palást
területét: |
Képlettel: |
 |
Behelyettesítve a kör kerület, terület és körcikk terület képletét
(r: alapkör sugara; R: palást
körcikkének sugara): |
Képlettel: |
 |
|
A
kúp térfogatát
úgy kaphatjuk meg, hogy az alap területét szorozzuk a kúp magasságával,
és a szorzatot osztjuk hárommal: |
Képlettel: |
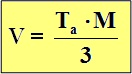 |
|
Behelyettesítve a kör terület képletét (r: alapkör
sugara): |
Képlettel: |
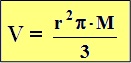 |
| |
|
|
|