Kör                                                                              

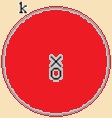
Egy ponttól (középpont) adott (ugyanakkora, de nem nulla) távolságra lévő pontok halmaza a síkban a körvonal.	Példa:
Egy ponttól adott (ugyanakkora, de nem nulla) távolságnál nem nagyobb távolságra lévő pontok halmaza a síkban a körlap vagy körlemez. (A körvonal és azon belüli pontok halmaza.) A körvonalat, körlapot illetve körlemezt is röviden körnek nevezzük.	Példa:
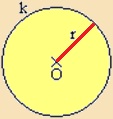
Azt a szakaszt, amely a kör középpontját a körvonal tetszőleges P pontjával köti össze, sugarának (latinul rádiusznak) nevezzük.           Jele:  r	Példa:
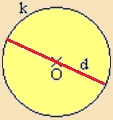
Azt a szakaszt, amely a körvonal két pontját köti össze, és tartalmazza a középpontot, a kör átmérőjének nevezzük. Az átmérő kétszer akkora, mint a sugár.           Jele:  d   [ (2 · r = d)	Példa:
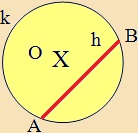
A kör bármely két pontját összekötő szakasz a húr. A kör középpontján átmenő húr a leghosszabb, és ez az átmérő.	Példa:
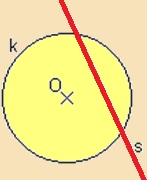
Azt az egyenest, amelynek egy körvonallal két közös pontja van, szelőnek nevezzük.	Példa:
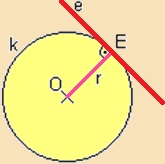
Azt az egyenest, amelynek egy körvonallal egy közös pontja van, érintőnek nevezzük. Az érintő mindig merőleges az érintési pontba húzott sugárra.	Példa:
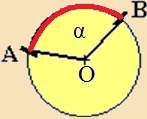
A körvonalat bármely két pontja két körívre bontja.           Körív hossza:	Példa:
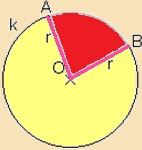
A körlemezt bármely két sugara két körcikkre bontja.           Körcikk területe:	Példa:
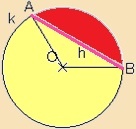
A körlemezt bármely húrja két körszeletre bontja.           Körszelet területe:           A hozzá tartozó körcikk területéből kivonjuk a sugarak és a hozzátartozó húr           által körbezárt háromszög területét.	Példa:
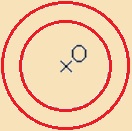
Az egyközéppontú (azonos középpontú) köröket koncentrikus köröknek nevezzük.	Példa:
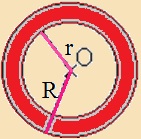
A koncentrikus körök közötti részt körgyűrűnek nevezzük. Körgyűrű területe: A két kör területének különbsége: T1 – T2 = R2π – r2 π = π · (R2 – r2)	Példa:

vissza a lap tetejére...