Bizonyítás:
A
B
csúcsnál levő szög
szögfelezőjének (f-nek)
a pontjai egyenlő
távolságra vannak az a
és a c oldal
egyenesétől.
A
C
csúcsnál levő szög
szögfelezőjének (g-nek)
a pontjai egyenlő
távolságra vannak az a
és a b oldal
egyenesétől.
Így az
f
és a g közös
pontja O,
egyenlő távolságra van háromszög
mindhárom oldalegyenesétől (a,
b és
c
oldalegyenesektől), tehát a
A csúcsnál
levő szög szögfelezője is O
pontban metszi a másik két
szögfelezőt.
Az
O pontból az oldalakra bocsátott merőleges
szakaszok egyenlők,
tehát az
O a beírható
kör középpontja, és a beírható kör sugara (r),
éppen ezek a merőleges szakaszok. |
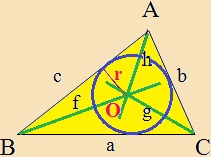
Ábra: |
 |