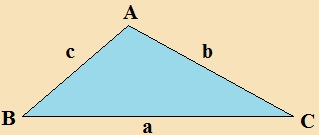
Sokszögek kerületén az oldalak hosszúságának összegét értjük, tehát a
háromszög kerülete:
K = a + b + c. |
Példa: |
 |
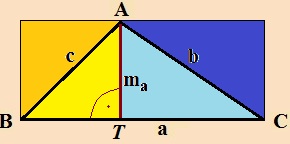
Vegyünk két egybevágó háromszöget. Az
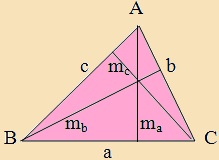
a oldalhoz tartozó magasság (ma),
a BC oldat T pontban metszi.
Az ma magasság
mentén „vágjuk ketté” az egyiket, így két háromszöget kapunk. (ABT
- világossárga és ATC - világoskék háromszögeket.). Egészítsük ki téglalappá a
háromszöget!
A sötétebb illetve a világosabb sárga háromszögek egybevágók, és a
világosabb illetve a sötétebb kék háromszögek is egybevágók. Ezért a
háromszög területe éppen a téglalap területének a fele. A téglalap
rövidebbik oldalának hossza megegyezik a háromszög magasságának
hosszával.
A téglalap területe: a · ma,
így a
háromszög területe:
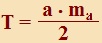 |
Példa: |
 |
Minden oldalhoz tartozik egy
magasság, ezért a
háromszög területe:
(alap szorozva a hozzátartozó magassággal) osztva 2-vel.
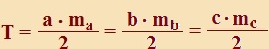 |
Példa: |
 |
|