|
| A |
az
„A”
halmaz elemeinek a száma
(halmazok
számossága) |
Példa: |
A
:=
{ 2; 4; 6; 8 } -->
| A | = 4
B
:=
{ 2; 3; 5; 7; 11; 13 }
-->
| B | = 6
C
:=
{ páros számok }
-->
| C | =
 |
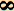kiegészítő (komplementer) halmaz
Egy „A” halmaznak az alaphalmazra vonatkozó kiegészítő (komplementer)
halmazán értjük azt a halmazt, melynek elemei az alaphalmaz összes olyan
eleme, amely nem eleme „A” halmaznak. |
Példa: |
 |
A = B
halmazok egyenlősége
Két halmazt akkor nevezünk egyenlőnek, ha minden elemük ugyanaz. |
Példa: |
A
:= { 2; 4; 6; 8 } és B
:= { 8; 6; 4; 2 }
ezért A = B |
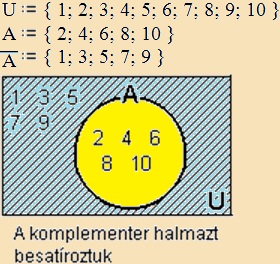
U
halmazok uniója (egyesítése)
Két vagy több halmaz uniója (egyesítése) pontosan azokat az elemeket
tartalmazza, amelyeket az egyik vagy másik (vagy mindegyik) halmaz. |
Példa: |
 |
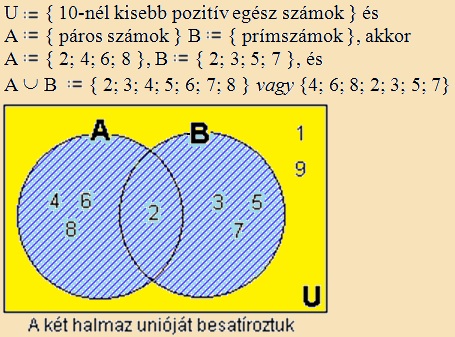halmazok metszete (közös
része)
Két vagy több halmaz metszete (közös része) pontosan azokat az elemeket
tartalmazza, amelyeket az egyik halaz is és a másik halmaz is tartalmaz. |
Példa: |
 |
|
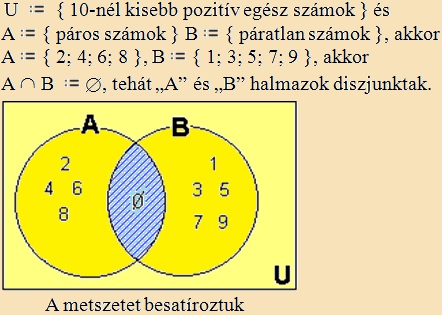
Ha két halmaznak nincs közös része, vagyis metszetük üres halmaz, akkor
a két halmazt diszjunkt
(idegen) halmazoknak nevezzük. |
Példa: |
 |
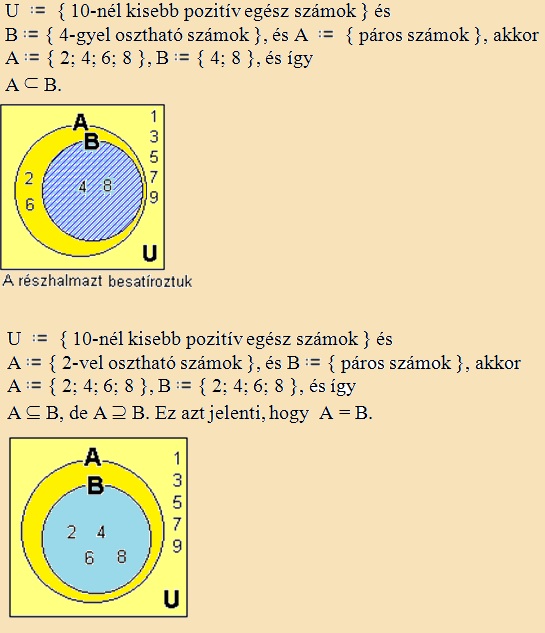
részhalmaz
Az „B” halmaz részhalmaza a „A” halmaznak, ha a „B” halmaz minden eleme
eleme az „A” halmaznak is. („B” halmaz „benne van” az „A” halmazban.) |
Példa: |
 |
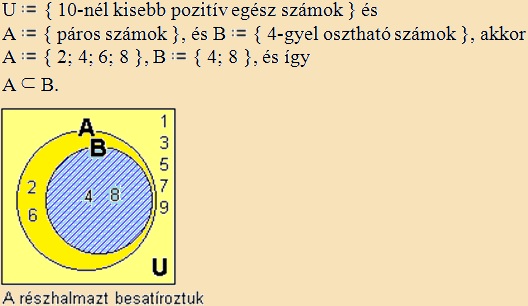
valódi részhalmaz
A „B” halmaz valódi részhalmaza az „A” halmaznak, ha az „B” halmaz
minden eleme eleme az „A” halmaznak is, de „A” halmaznak legalább egy
olyan eleme van, amelyik nem eleme a „B” halmaznak. |
Példa: |
 |
\
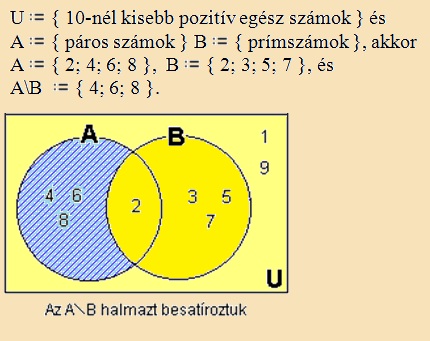
különbség halmaz
(differencia)
Két halmaz különbség halmaza pontosan azokat az elemeket tartalmazza,
amelyeket az egyik a kisebbítendő halmaz tartalmaz, de a kivonandó
halmaz nem. (Ezt úgy is értelmezhetjük, hogy a kisebbítendő halmazból
elvesszük a két halmaz közös részét.)
A\B
:= A\ (A
B) |
Példa: |
 |
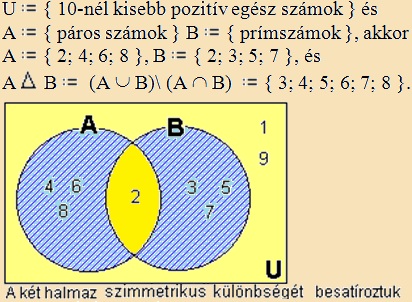
szimmetrikus különbség halmaz
Két halmaz szimmetrikus különbség halmaza pontosan azokat az elemeket
tartalmazza, amelyek vagy csak az egyik halmaz tartalmaz vagy csak a
másik halmaz tartalmaz. (Ezt úgy is értelmezhetjük, hogy a két halmaz
uniójából elvesszük a két halmaz közös részét.)
A
B
:=
(A
U B) \ (A
B) |
Példa: |
 |
A X B
direkt szorzat
Két halmaz „A” és „B” direkt szorzata mindazon rendezett két elemű
halmazok, melynek első tagja az „A” halmazból, második tagja a „B”
halmazból kerül ki. |
Példa: |
U
:= { 10-nél kisebb pozitív egész számok } és
A := { páros számok }; B := { páratlan számok }, akkor
A := { 2; 4; 6; 8 }, B := { 1; 3; 5; 7; 9 }, ekkor
A X B := { 2 ; 1 }; {
2 ; 3 }; { 2 ; 5 }; { 2 ; 7 }; { 2 ; 9 };
{ 4 ; 1 }; {
4 ; 3 }; { 4 ; 5 }; { 4 ; 7 }; { 4 ; 9 };
{ 6 ; 1 }; {
6 ; 3 }; { 6 ; 5 }; { 6 ; 7 }; { 6 ; 9 };
{ 8 ; 1 }; {
8 ; 3 }; { 8 ; 5 }; { 8 ; 7 }; { 8 ; 9 }. |
