|
N
[
a
természetes számok halmaza |
Példa: |
N
:= { 0; 1; 2; 3; 4; 5; 6; 7; 8 ... } |
|
N+
[
a pozitív egész
számok halmaza |
Példa: |
N+
:= { 1; 2; 3; 4; 5; 6; 7; 8 ... } |
|
Z
[
az egész
számok halmaza |
Példa: |
Z
:= { ... -4; -3; -2; -1; 0; 1; 2; 3; 4
... } |
Q
[
a racionális
számok halmaza
Minden olyan szám, melyik felírható két egész szám hányadosaként.
Ide tartoznak az egész számok, véges
tizedes törtek, végtelen
szakaszos tizedes törtek, közönséges
törtek. |
Példa: |
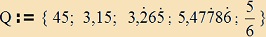 |
Q+
[
az irracionális
számok halmaza
Minden nem racionális szám. Ide tartoznak a végtelen nem
szakaszos tizedes törtek. |
Példa: |
Q*
:= {5,12567358...; 2,12112111… p. } |
R
[
a valós
számok halmaza
A racionális és irracionális számok halmaza együtt. |
|
|
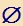 [
az üres
halmaz
[
az üres
halmaz
Olyan halmaz, amelynek nincs egyetlen eleme sem. |
Példa: |
A Holdon élő emberek halmaza. |
U
[
az alaphalmaz
(Univerzum)
Az a halmaz, melyből a feladatban szereplő halmazok elemei
kikerülhetnek. |
Példa: |
Ha U { 10-nél kisebb pozitív számok } és A := { páros számok }, az „A” halmaz
elemei lehetnének a 10; 12; 14; ... számok is, de ez az alaphalmazban
nincs benne, így a feladat megoldása sem lehet, így csak az {1; 2; 3; 4;
5; 6; 7; 8; 9} számokból kerülhetnek ki az "A" halmaz elemei! |