| Lásd még: Kúp | |
|
|
A gúla olyan test, amelyet egy sokszöglap és annyi egy csúcsba összefutó háromszöglap határol, ahány oldala van a sokszögnek. A sokszög a gúla alapja, a háromszögek a gúla oldallapjai. Az alapokat határoló élek az alapélek. Az oldallapok az oldalélekben találkoznak. Az oldalélek egy pontban, a gúla csúcspontjában (csúcsában) futnak össze. Az oldallapokat együtt a gúla palástjának nevezzük. Oldallapmagasság: a palást egy háromszögének (oldallapjának) a magassága. Testmagasság: a csúcsból az alap síkjára bocsátott merőleges szakasz hossza. |
Példa: |
 |
|
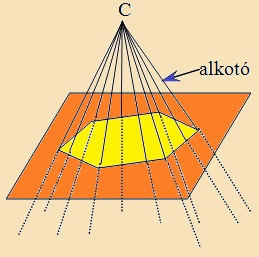
Gúlafelületet
kapunk, ha a sokszögvonal minden pontján át egy, a sokszög síkján kívül levő C pontból félegyeneseket húzunk. A gúlafelületnek a C pont és a sokszög közötti részét gúlának nevezzük. A sokszögvonal pontjai és a csúcs közötti szakaszok a gúla alkotói. Így az oldalélek is alkotók. |
Példa: |
 |
|
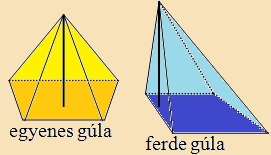
Az
egyenes gúla
oldalélei egyenlő hosszúak, tehát oldallapjai egyenlőszárú háromszögek. A ferde gúla oldalélei nem egyenlő hosszúak. |
Példa: |
 |
|
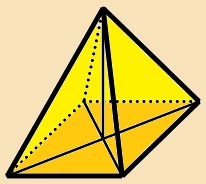
A
szabályos gúla
alapja szabályos sokszög, oldalélei egyenlő hosszúak, tehát oldallapjai
egybevágó egyenlőszárú háromszögek, és az alappal alkotott hajlásszögük is
egyenlő. Az n oldalú gúlának (n+1) számú lapja, (n+1) számú csúcsa és 2n számú éle van. |
Példa: |
 |
| A gúla felszínét úgy kaphatjuk meg, hogy az alap területéhez hozzáadjuk a palást területét. | Példa: |
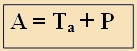 |
| A gúla térfogatát úgy kaphatjuk meg, hogy az alap területét szorozzuk a gúla magasságával, és a szorzatot osztjuk hárommal. | Példa: |
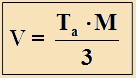 |