Egyenlőtlenség                                                            

Egyenlőtlenség: Olyan nyitott mondat, amelyben két kifejezést a <, >, ≤, ≥, ≠ jel valamelyike köt össze.
Az egyenlőtlenség mindkét oldalának azonos változatásával egyre egyszerűbb egyenlőtlenséget kapunk, végül az egyik oldalon csak az ismeretlen, a másik oldalon csak az ismert mennyiség áll. Az egyenlőtlenség ekkor megoldott.
Szabad az egyenlőtlenség minkét oldalához hozzáadni (+) vagy kivonni (-) számot vagy ismeretlen kifejezést.
Szabad az egyenlőtlenség minkét oldalát szorozni (∙) vagy osztani (:) pozitív számmal vagy pozitív ismeretlen kifejezéssel.
Ha az egyenlőtlenség mindkét oldalát szorozzuk (∙) vagy osztjuk (:) negatív számmal vagy negatív ismeretlen kifejezéssel, az egyenlőtlenség iránya megfordul.
Nullával nem szabad az egyenlőtlenség oldalait szorozni. (Osztani értelmetlen nullával!)
Egyenlőtlenséget ugyanúgy oldunk meg, mint az egyenleteknél tanultuk, de figyeljünk a negatív számmal való szorzásra és osztásra. Csak az ellenőrzésben tér el.
Az olyan egyenlőtlenséget, amelyben az ismeretlen minden helyére bármilyen számot behelyettesítve az egyenlőtlenség igaz lesz, (minden számra igaz,) azonos egyenlőtlenségnek nevezzük.	Példa:	x + x + x > 2x
Az olyan egyenlőtlenséget, amelyben az ismeretlen minden helyére bármilyen számot behelyettesítve az egyenlőtlenség sose lesz igaz, (semmilyen számra sem igaz,) ellentmondásnak nevezzük, és nincs megoldása az egyenlőtlenségnek.	Példa:	x + x ≤ x
Az egyenlőtlenség igazsághalmazán értjük azt a számhalmazt, amely az egyenlőtlenség összes megoldását (gyökét) tartalmazza.
	Példa:
1) Ahol a tört számlálójában többtagú kifejezés szerepel, tegyük ki a     zárójeleket. Ahol egész számot találunk, írjunk a nevezőbe 1-et.	Példa:
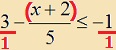2) Bővítsük a törteket úgy, hogy a nevező mindenütt egyforma (5)     legyen.	Példa:
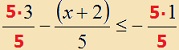3) Szorozzuk meg az egyenlet mindkét oldalát a közös nevezővel    (5-tel), így eltűnik a nevező. (Másoljuk le a számlálót!)	Példa:
4) Bontsuk fel a zárójeleket.	Példa:
5) Vonjunk össze oldalanként.	Példa:
6) Kevesebb ismeretlent vigyük a másik oldalra      (mindkét oldal azonos változtatásával).	Példa:	(ha van - itt most nincs!)
7) Az ismeretlen mellől vigyük a számot a másik oldalra     (mindkét oldal azonos változtatásával).	Példa:
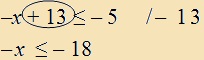8) Osszuk el mindkét oldalt az ismeretlen előtti számmal     (együtthatóval azaz (-1)-gyel!), így megkapjuk az egyenlőtlenség     megoldását.	Példa:
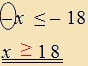9) Ábrázoljuk számegyenesen is.	Példa:
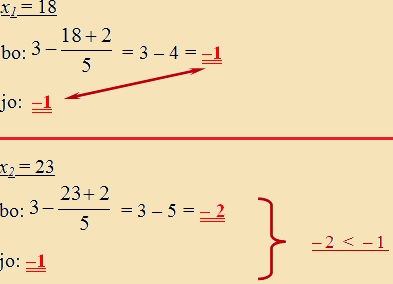
10) Ellenőrizzünk!        a) Helyettesítsük be az eredeti egyenlőtlenség jobb, majd bal            oldalán található ismeretlen helyére a kapott számot, és            nézzük meg, hogy a két oldal egyenlő-e.        b) Válasszunk ki a megoldáshalmazból (igazsághalmazból)            egy számot, helyettesítsük be az eredeti egyenlőtlenség            jobb, majd bal oldalán található ismeretlen helyére, és nézzük            meg, hogy a baloldal valóban olyan relációban áll-e a            jobb oldallal, mint az eredeti egyenlőtlenségben.	Példa: