Közönséges törtek                                                      

Közönséges tört értelmezése:
Nevező: megmutatja, hogy hány egyenlő részre osztjuk az egészet:	Példa:	4
Számláló: „megszámlálja”, hogy hány szelet a miénk az egyenlő                   részekből:	Példa:	3
Törtvonal: osztást jelent:	Példa:	3 : 4
1-nél nagyobb a tört, ha a számlálója nagyobb, mint a nevezője.	Példa:
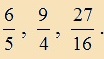1-gyel egyenlő a tört, ha a számlálója egyenlő a nevezőjével.	Példa:
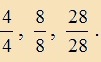1-nél kisebb a tört, ha a számlálója kisebb, mint a nevezője.	Példa:
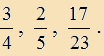Egészrész: a számban lévő legnagyobb egész szám.	Példa:
Az 1-nél nagyobb törteket áltörteknek hívjuk.
Az áltörteket felírhatjuk vegyes szám alakba a következő képen: A számlálót maradékosan elosztjuk a nevezővel, a hányados lesz az egészrész, a maradék a törtrész számlálója, a nevező változatlan. Példa: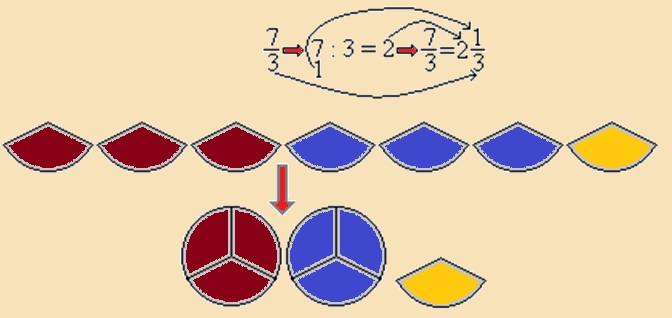
Vegyes számból a következő képen lesz áltört: Az egészrészt szorozzuk a nevezővel, hozzáadjuk a számlálót, ez lesz az új számláló, a nevező pedig változatlan. Példa:
A törtet kétféleképpen értelmezhetjük:
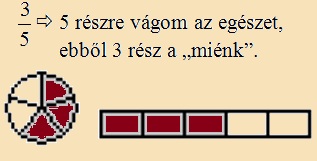
a) Annyi részre vágjuk az egészet, amennyi a nevező, majd annyi     egyenlő rész a „miénk”, amennyi a számláló.	Példa:
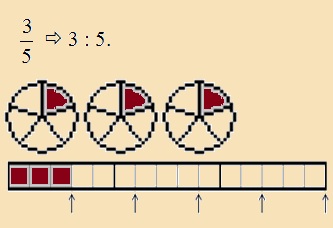
b) Számláló osztva nevezővel.	Példa:
Törtek ellentettje: A szám. (–1) –szerese.
Pozitív számnak a negatív párja.	Példa:
Negatív számnak a pozitív párja.	Példa:
Nulla (0) ellentettje nulla (0).
Jele: – a
Tört számok abszolút értéke: Nullától (0) való távolságot jelent a számegyenesen.
Pozitív számnak és nullának önmaga.	Példa:
Negatív számnak a pozitív párja (ellentettje).	Példa:
Jele: | a |
Egyszerűsítés, bővítés: katt!
Közös nevezőre hozás: katt!
Törtek összehasonlítása: katt!
Törtek összeadása és kivonása: katt!
Törtek szorzása: katt!
Törtek osztása: katt!