| A mértani sorozat a számok olyan sorozata, amelyben bármelyik számot az előzővel osztva, a hányados állandó. | Példa: |
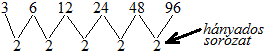 |
| Jelölések: | ||
| - A hányados sorozat elemei, a hányados, vagy qvociens. | Jele: | q |
|
-
Mértani
sorozat n-edik elemét
úgy kaphatjuk meg, hogy az első elemét megszorozzuk a hányados (n ‑ 1) - edik hatványával. |
Képlettel: |
|
| - A mértani sorozat első n elemének összege: | Képlettel: |
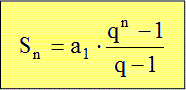 |
|
- A mértani
sorozatban az első elemet kivéve, bármely tag a két szomszédjainak a mértani közepe. (Mértani közép: kép szám szorzatából vont négyzetgyök) Általában az n-edik tag (an) a tőle balra illetve jobbara ugyanannyi hellyel álló tagok (an-k; an+k) mértani közepe. |
Példa: |
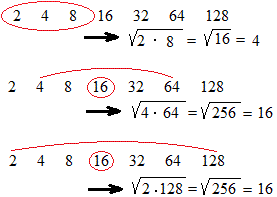 |