|
Tétel megfordítása:
Ha egy háromszög leghosszabb oldalára rajzolt négyzet területe egyenlő a
két rövidebb oldalakra rajzolt négyzetek területeinek összegével, akkor
a háromszög derékszögű. |
||
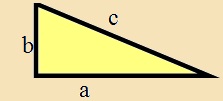
| Bizonyítás: Legyen a szóban forgó háromszög két rövidebb oldala a és b, a leghosszabb, pedig c. Erre igaz a következő állítás: a2 + b2 = c2. | Példa: |
 |
|
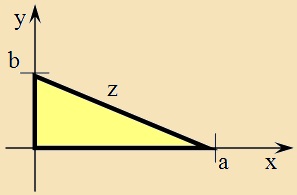
Rajzolunk egy derékszögű koordináta rendszert. Az egyik tengelyére
mérjünk fel egy a
hosszúságú szakaszt az origótól kiindulva, a másik tengelyére pedig egy
b
hosszúságú szakaszt, szintén az origótól kiindulva. Kössük össze a
szakaszok végpontjait, ezt a szakaszt jelöljük
z -vel. Ez a
háromszög derékszögű, tehát igaz rá Pitagorasz tétele: a2 + b2
= z2. Az első háromszögre igaz a következő állítás: a2 + b2 = c2. A második háromszögre igaz a következő állítás: a2 + b2 = z2. Ekkor viszont c2 = z2. Mivel c és z oldalakat jelölnek, nem lehetnek negatívak, ezért c = z. Tehát a két háromszög oldalai rendre megegyeznek, ezért a két háromszög egybevágó, s ezzel a tétel megfordítását igazoltuk. |
Példa: |
 |