|
Tétel:
A derékszögű háromszög befogóira rajzolt négyzetek területeinek összege
egyenlő az átfogóra rajzolt négyzet területével. a2 + b2 = c2 |
Példa: |
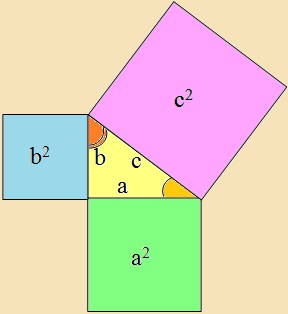 |
| Bizonyítás: Az a+b oldalú négyzetbe rajzoljuk be az a2 és b2 területű négyzeteket az ábrához hasonlóan, illetve a 4 db, eredetivel is egybevágó derékszögű háromszögeket. | Példa: |
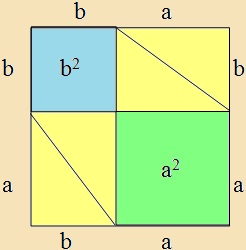 |
|
Egy másik a+b
oldalú négyzetbe a másik ábrához hasonlóan rajzoljuk be 4 db, eredetivel is egybevágó derékszögű háromszögeket. A belül keletkezett négyszög biztosan rombusz, hiszen minden oldala c hosszúságú. A derékszögű háromszög két hegyesszögének összege (α + β =) 90º. A rombusz csúcsa mellett egy és α egy β szög található. Ezért a rombusz szöge csak γ = 90º-os lehet (hiszen α + β + γ = 180º), és ez minden szögére igaz, tehát ez a rombusz négyzet. Ezzel a tételt bizonyítottuk. |
Példa: |
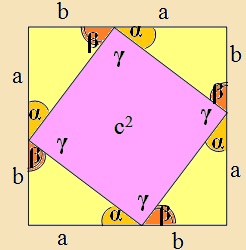 |