Forgatás                                                                       

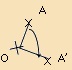
Definíció:	Olyan egybevágósági transzformáció, amely a középponthoz (O) önmagát rendeli, minden középpontra nem illeszkedő P ponthoz olyan P’ pontot rendel, amelynél a P és P’ pontok illeszkednek egy előre megadott irányított szög kezdő és végszárára, a szög csúcsa pedig az O középpont és OP = OP’.
Fix pontok:	A középpont (O) képe önmaga.
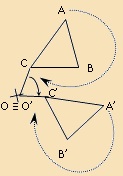Egyértelműen adott:	- Középponttal és egy irányított szöggel. - Pontpárral és középponttal. - Pontpárral és egy irányított szöggel.
Körüljárási irányt...	megtartja
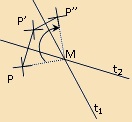
Helyettesíthető:	Két egymást metsző tengelyes tükrözés egymásutánjával. Az irányított szög nagysága a tengelyek szögének kétszerese, iránya a t1, t2 iránya.
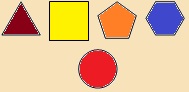
Alakzatok, melyre a transzformációt alkalmazva önmagába megy át:	Forgásszimmetrikus alakzatok: - szabályos sokszögek - kör. -
Egybevágósági transzformáció, tehát...
Egyéb:	- A középponton átmenő egyenes képe is átmegy a középponton. - Metszéspont képe a képalakzat metszéspontja.